News

• *** GLMdenoise is a subset and has been superseded by a new tool called GLMsingle. Users are encouraged to study and explore that new tool. Nonetheless, the content available here is still valid and will be preserved for informational purposes. ***
  
• 2014/08/01 - Release of version 1.4.
• 2014/07/14 - Release of version 1.31.
• 2013/12/13 - Release of version 1.3.
• 2013/12/12 - Three new example scripts added.
• 2013/12/06 - GLMdenoise paper published.
• 2013/11/18 - Release of version 1.2.
• 2013/05/12 - Release of version 1.1. Many new useful features.
• 2013/05/10 - A new FAQ with many useful bits of information (see below).

History of major code changes

• 2014/08/01 - Version 1.4. Add option for obtaining parametric GLM fits and error estimates. Add new DVARS sanity-check figures. Change polynomial functions such that they are all mutually orthogonal and unit-length (this may cause slight changes to behavior due to numerical precision issues).
• 2014/07/14 - Version 1.31. Minor fixes to improve platform compatibility.
• 2013/12/13 - Version 1.3. Added new example scripts.
• 2013/11/18 - Version 1.2. The default canonical HRF has changed. (It is now smoother/nicer than before.) If pcvoxels is determined to be empty (e.g. no voxels were above 0% for any number of PCs), we now issue a warning (instead of crashing) and fallback to simply using the top 100 voxels to select the number of PCs. Use fullfile to ensure compatibility with different platforms.
  
• 2013/05/12 - Version 1.1. The experimental design can now be specified in terms of onset times.
  This means that conditions do not have to exactly coincide with the TRs. Fixed a bug concerning extraregressors. Additional optional inputs, additional outputs, and additional figures. All-zero regressors (e.g. encountered via bootstrapping) are now assigned zero weight.
• 2012/12/03 - Version 1.02. Various speed-ups and minor bug fixes.
• 2012/11/24 - Version 1.0.

Introduction

GLMdenoise is a technique for denoising task-based fMRI data. The basic idea is to derive noise regressors from voxels unrelated to the experimental paradigm and to use these regressors in a general linear model (GLM) analysis of the data. The technique does not require external physiological monitoring nor does it require extra fMRI data—thus, it can be retrospectively applied to existing datasets. The technique is described in the following paper:

Kay, K.N., Rokem, A., Winawer, J., Dougherty, R.F., & Wandell, B.A. GLMdenoise: a fast, automated technique for denoising task-based fMRI data. Frontiers in Neuroscience (2013).

The technique is fast and automated and general: it requires only a design matrix indicating the experimental design and an fMRI dataset. The technique does make a few assumptions, however. First, it assumes that voxels unrelated to the experimental paradigm are contained in the dataset (e.g. voxels in other brain areas, white matter, etc.). Second, the technique assumes that there are at least two runs available and that experimental conditions are repeated across runs. This requirement is necessary because GLMdenoise involves cross-validation across runs.

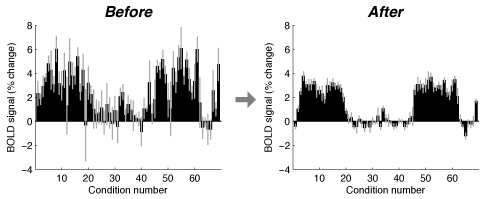
The amount of improvement in signal-to-noise ratio (SNR) provided by GLMdenoise depends on a variety of factors, such as the intrinsic SNR level, the amount of data collected, and the experimental design. We suspect that SNR gains will tend to be more substantial for low-SNR regimes such as event-related experiments where stimulus durations are brief and evoked fMRI responses are small.

We provide MATLAB code implementing GLMdenoise. The code consists of standard (uncompiled) MATLAB functions, takes advantage of MATLAB's built-in multithreading, and requires only the Statistics Toolbox. The code has been tested on MATLAB 7.6 and 7.9, and should probably work with any recent version of MATLAB.

If you use GLMdenoise in your research, please cite the above paper.

Getting started

Get code from github
After downloading and unzipping the files, launch MATLAB and change to the directory containing the files. You can then run the example scripts by typing "example1", "example2", etc. More information on the example scripts is provided below.

Download example dataset (82 MB)
This dataset is required to run the example scripts. Place the dataset inside the code directory. Alternatively, the example scripts will automatically download the dataset.

Join the GLMdenoise discussion group
This mailing list is for anyone interested in using the GLMdenoise toolbox. Announcements regarding GLMdenoise will be made to this mailing list.

Browse code in HTML (version 1.4)

Basics of the code

The input and output format of the code is intentionally generic. We would be happy to help integrate the code with existing analysis packages.

Inputs. The code requires the following inputs:

• 'design' - This is a design matrix that indicates the experimental design. The dimensions are time x conditions. Each column corresponds to one condition and should consist of 0s except for 1s indicating the onset of the condition. To indicate design matrices for multiple runs, construct a cell vector like { design1 design2 design3 ... }. Alternatively, the experimental design can be specified in terms of onset times. This allows cases where conditions do not exactly coincide with the TRs of the data. The format is {{C1_1 C2_1 C3_1 ...} {C1_2 C2_2 C3_2 ...} ...} where Ca_b is a vector of onset times (in seconds) for condition a in run b. Time starts at 0 and is coincident with the acquisition of the first volume. Note that if you use the onset-time specification of the experimental design, you will be forced to assume a fixed HRF.
• 'data' - This is the fMRI time-series data. The dimensions are X x Y x Z x time (which indicates that the data has 3D structure); alternatively, the dimensions can be voxels x time (but in this case, some figures will not be informative to look at). The data should contain finite values (e.g. no NaNs) and should be in single-format (if not, we automatically convert to single-format). Voxels with invalid data can be set such that their time-series consist of all 0s. To indicate data for multiple runs, construct a cell vector like { data1 data2 data3 ... }.
• 'stimdur' - The duration of a condition in seconds (e.g. 3). This input is used only to generate an initial seed for the HRF.
• 'tr' - The sampling rate (TR) of the data in seconds (e.g. 2).

Note that the fMRI data should already be pre-processed. We recommend that at a minimum, slice time correction and motion correction should be performed and the first few volumes of each run should be discarded to allow magnetization to reach steady-state. We do not recommend detrending or high-pass filtering the time-series; this is because polynomial regressors are included in the GLM and it is more accurate to model low-frequency fluctuations as part of the GLM. Spatial smoothing and/or atlas normalization are fine as pre-processing steps.

Hint: Make sure that you have discarded the first few volumes of each run (to avoid initial magnetization effects) and that your data matrices do not have any NaNs. Also, make sure that your data has not been mean-subtracted (or converted to percent BOLD change). For example, if you view a slice of your data, your data should look like a brain (values should largely be positive).

Code execution. The most basic call to the code is:

[results,denoiseddata] = GLMdenoisedata(design,data,stimdur,tr,[],[],[],'figures');

This command writes diagnostic figures to the directory 'figures' and returns outputs in 'results' and 'denoiseddata'.

Outputs. The code produces the following outputs:

• 'results' - This contains the GLM analysis results, including estimates of the hemodynamic response function (HRF) and estimates of BOLD response amplitudes (beta weights). The 'results' variable is a struct --- it may be useful to use the "-struct" functionality of the MATLAB save command when saving the results to disk.
• 'denoiseddata' - This contains the denoised data, that is, the time-series data with the component of the data that is estimated to be due to the global noise regressors removed. The point of this output is to make it easy for the code to be integrated into existing analysis workflows (i.e., the user can choose to ignore the GLM analysis results and treat the code as a pre-processing step prior to subsequent data analysis). However, there are important caveats to this type of usage (see FAQ for details).

For additional details on the code outputs, please see the documentation in GLMdenoisedata.m.

Example scripts

Example dataset. The example scripts make use of an example dataset. The example dataset consists of fMRI measurements in human visual cortex at 3T using gradient-echo, isotropic 2.5-mm voxels, and a TR (sampling rate) of approximately 1.3 s (1.337702 s). The dataset has a dimensionality of 64 voxels x 64 voxels x 4 slices. (The original dataset contains 22 slices, but we have extracted slices 9–12 to make the dataset smaller in size.) The data have been pre-processed, including discarding the first few volumes of each run, slice time correction, motion correction, and spatial undistortion based on fieldmap measurements. Voxels for which a complete set of data is not available (e.g. due to head motion) have been set such that their time-series consist of all 0s. The following variables are contained in the dataset file:

• 'design' - This is a cell vector of dimensions 1 x 10. Each element of the cell vector is a design matrix of dimensions 265 time points x 35 conditions. The format is double and values are either 0 or 1.
• 'data' - This is a cell vector of dimensions 1 x 10. Each element of the cell vector is an fMRI run of dimensions 64 voxels x 64 voxels x 4 slices x 265 time points. The format is single (to save on memory usage).
• 'stimdur' - This is a scalar (3), indicating the duration of each condition in seconds.
• 'tr' - This is a scalar (1.337702), indicating the sampling rate (TR) in seconds.

Example scripts. The following links are to HTML pages automatically produced by the MATLAB publish command.

• Example 1: Run GLMdenoise on an example dataset.
• Example 2: Analyze different splits of runs in a session.
• Example 3: Run GLMdenoise using finite impulse response (FIR) model.
• Example 4: Use GLMdenoise, allowing voxel-specific HRFs.

Frequently asked questions (FAQ)

• "How does GLMdenoise compare to incorporating motion regressors, physiologically-derived regressors (e.g. RETROICOR), etc., into a standard GLM analysis?"
  
  This issue is discussed in the manuscript. An advantage of GLMdenoise is that it subsumes these sorts of effects and is therefore more general. For example, if some portion of the noise can be modeled away using motion parameters, then this in theory can be derived directly from the data using the GLMdenoise technique. Furthermore, GLMdenoise has the advantage of being self-calibrating. Including nuisance regressors in a GLM may actually degrade accuracy due to overfitting. GLMdenoise uses cross-validation and therefore automatically determines the appropriate number of nuisance regressors to include.
  
  As shown in the manuscript, GLMdenoise outperforms the strategy of including motion parameters as nuisance regressors and the strategy of using physiological regressors (RETROICOR). Note that one caveat is that we are under the working assumption that subject motion is not reliably correlated with the task. The case of task-correlated motion is complicated and dealing with this problem effectively is outside the scope of the GLMdenoise technique.
  
  On a practical note, since GLMdenoise already deals with a variety of noise effects, you do not need to (and you should not) attempt to supply noise regressors (e.g. motion parameters, drift parameters) to GLMdenoise. All you need to supply is a specification of the experimental design matrix.
  
  
• "I have read about ICA (independent components analysis) as a potential denoising technique. How does GLMdenoise compare?"
  
  At some level, GLMdenoise and ICA are similar techniques, as they are both data-driven techniques that attempt to isolate and remove noise. However, ICA relies on certain assumptions for identifying different components of the data, and there is no guarantee that the signal (i.e. portions of the data related to the task) and the noise are accurately identified. GLMdenoise explicitly estimates the portion of the data that is related to the experiment (through a GLM analysis) and uses cross-validation to verify that these estimates are accurate. Of course, depending on the nature of the data and the goals of the analysis, ICA may have its own advantages (e.g. the fact that it is model-free may be an advantage in cases where a model of the experiment is unknown). A direct comparison of ICA and GLMdenoise is provided in the manuscript.
  
  
• "The conditions in my experiment have different durations (e.g., a 2-s stimulus, a 6-s stimulus, etc.). How can I use GLMdenoise to deal with this situation?"
  
  The underlying model of GLMdenoise is that the design matrix (which consists of 1s that indicate the onsets of different conditions) is convolved with a timecourse (the HRF) to obtain the predicted effects of the various conditions on the BOLD signal. To characterize the fact that the response to a 6-s stimulus is expected to have a longer duration than the response to a 2-s stimulus, we can simply code the design matrix appropriately. For example, suppose the TR (data sampling rate) is 1 s. Then, the column in the design matrix corresponding to the 2-s stimulus can be simply coded as something like [0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0] where 1 indicates the onset of the 2-s stimulus. The column in the design matrix corresponding to the 6-s stimulus can be coded as something like [0 0 0 0 0 0 0 0 1 0 1 0 1 0 0 0] where the first 1 indicates the onset of the 6-s stimulus and the two additional 1s occur 2 s and 4 s after the initial onset. The idea is that there is a fixed timecourse associated with 2-s of stimulation and that the response to the 6-s stimulus is assumed to be obtained by shifting and summing this timecourse appropriately. Be aware that the interpretation of the beta weights associated with the 2-s and 6-s conditions is a little tricky --- the beta weight associated with the 2-s stimulus is simple (as it is just a scale factor that is applied to the HRF (which is normalized to peak at one)), but the beta weight associated with the 6-s stimulus is more complicated. The predicted response to the 6-s stimulus is given by first shifting and summing the HRF and then scaling by the beta weight. Because of the shifting and summing, the timecourse that is associated with the 2-s stimulus (before beta weight scaling) differs in shape and amplitude from the timecourse that is associated with the 6-s stimulus (before beta weight scaling).
  
  A totally different strategy for dealing with different duration conditions is to use a finite impulse response (FIR) model (see example scripts).
  
  
• "If I want to model events with different intensity, can I just replace the 1s in the design matrix with the appropriate fractions?"
  
  Yes, the design matrix does not have to consist of only 1s and 0s, but can include fractional values as well. The case of fractional values is treated exactly as expected --- for example, if one event onset is coded as 1.0 and another onset of that same event is coded as 0.5, then the model enforces the expectation that the amplitude of the response resulting from the second onset will be half as large as the amplitude of the response resulting from the first onset.
  
  
• "I typically spatially smooth my data. Is that compatible with GLMdenoise?"
  
  Yes, it is compatible, and you can treat smoothing as a pre-processing step that is applied to the data prior to the application of GLMdenoise.
  
  One benefit of smoothing is that it generally improves SNR. The GLMdenoise technique also improves SNR. On datasets that I have experimented with, I have found that GLMdenoise improves SNR both on unsmoothed and smoothed data. This makes sense since the type of noise removed by GLMdenoise (large-scale correlated noise) is different than the noise removed by smoothing (local uncorrelated noise).
  
  
• "I like to use multivariate pattern analysis (i.e. pattern classifiers) on my fMRI data. Can GLMdenoise help me?"
  
  Yes, it can. The intuition is that more information can be extracted (i.e. decoded) from the data if the data have less noise. However, it is important to think carefully about the issue of how exactly a given pattern analysis model is trained and tested in a given experiment. When applying GLMdenoise to a set of runs, all runs in that set contribute to the final results, and so the runs are no longer independent.
  
  One approach for separating training and testing data in the context of a multivariate pattern analysis is to cross-validate across runs. For example, suppose 10 runs of data are collected. A model can be trained from 5 runs and then tested on the other 5 runs. To integrate this approach with GLMdenoise, one could separately apply GLMdenoise to each set of 5 runs. This way, there is no interaction between the data in the two sets of runs.
  
  An additional issue that may be interesting to consider in the context of multivariate pattern analysis is that GLMdenoise is based on the concept of removing correlated noise across voxels. When applying pattern analysis to a set of voxels, the results will be affected by the extent to which noise is correlated across voxels and the extent to which these noise correlations are taken into account by the pattern analysis. After applying GLMdenoise to a set of data, not only is the overall level of noise likely to be reduced, but also the noise correlations are likely to be reduced.
  
  
• "Can I change the HRF model?"
  
  For simplicity, the default mode of operation for GLMdenoise is to assume that there is a common response timecourse (the HRF) that is shared across all conditions and voxels. The shape of this HRF is optimized to best fit the data (but can also be pre-specified and fixed by the user).
  
  A different approach is to attempt to tailor the shape of the HRF to individual voxels (or groups of voxels) (see example scripts).
  
  Yet another approach is to fully tailor the shape of the HRF for all conditions and all voxels. This can be done by using the finite impulse response (FIR) model (see example scripts).
  
  The GLMdenoise approach is applicable irrespective of the particular HRF model used (for example, gains in cross-validation performance and SNR can still be obtained if one decides to use an FIR model).
  
  
• "What if I have only one run of data?"
  
  GLMdenoise needs multiple runs so that it can perform cross-validation. So, if you have only one run, you will not be able to use GLMdenoise. However, if you split a run into two smaller successive runs before calling GLMdenoise, then that may be a potential solution. One issue with this strategy is that the experiment-related effects from the end of the first small run may spill over to the beginning of the next small run, and if you split a run before calling GLMdenoise, then GLMdenoise will not know about these spillover effects. Whether or not the spillover is a significant problem depends on the situation (e.g. how much spillover, how much data is collected, etc.), so this is something to think about.
  
  
• "My experiment consists of trials that are all unique (e.g., a given trial is never repeated elsewhere in the experiment (or I want to estimate the response to each trial separately)). Can I use GLMdenoise?"
  
  The code relies on cross-validation, and if conditions are never repeated, then a GLM cannot predict left-out data. So, GLMdenoise cannot be applied in this situation.
  
  
• "The idea that GLMdenoise can return the original data but with noise components removed (the 'denoised data') is nice and I am using the code that way. However, I have noticed some weird issues in my results."
  
  If you choose to apply GLMdenoise using the "data-to-data-transformation" approach, it is very important to keep in mind that quantities that depend on error estimates (e.g. t-values, p-values) derived from the denoised data will be invalid. To see why this is the case, imagine that the code just returned "noiseless" data, i.e. data consisting of just the estimated experimental effects. Then, using some post-hoc analysis of the denoised data (e.g. another GLM), the estimated noise level will be zero and t-values will be infinite, and this is clearly absurd. One way forward would be to just use the denoised data to derive best possible estimates of the main quantities of interest (e.g. beta weights) and to infer error on these estimates by looking across different sets of data. For example, the error can be inferred by looking at how the quantities of interest change in an independently analyzed set of runs, how the quantities change across subjects, etc. Another way forward is to abandon the "data-to-data-transformation" approach and just use the estimates of beta weights and standard error provided by GLMdenoise.
  
  
• "In looking at the scatter plots of cross-validation performance for different numbers of PCs, I find that performance on average improves across voxels, but some voxels degrade in performance. Is this a concern?"
  
  The metric of cross-validated R², like any metric, is sensitive to the amount of data that goes into the calculation of the metric. With sufficient amounts of data, random fluctuations (i.e. noise) in the left-out data will tend to average out in the calculation of the metric and the metric will tend to be robust. With small amounts of data, however, the metric may be noisy. Thus, there are two potential explanations for why cross-validation performance varies across voxels. One is that the underlying improvements are indeed consistent across voxels, and it is simply noise in the left-out data that is inducing variability in the observed cross-validation performance. The other is that voxels have real variability in their characteristics (e.g. some voxels have different denoising needs compared to other voxels). The reality is probably some combination of these two explanations, although we know a priori that with large datasets (i.e. many TRs, many runs), the first explanation has less influence. If you are particularly concerned with optimizing performance for a particular set of voxels, you can use opt.pcR2cutoffmask to specify the voxels to consider in the selection of the number of PCs to use.
  
  
• "I noticed that some voxels outside the brain have positive cross-validation values. Why is this?"
  
  As noted in the previous point, because noise affects the data used for cross-validation, cross-validated R² values are susceptible to noise. The threshold of a cross-validated R² value of 0% (which is used in the GLMdenoise technique at several points) is just a threshold, and false positives are still possible. That is, a voxel with no actual relationship to the experiment may, due to chance, have a cross-validated R² value greater than 0%.
  
  
• "The cross-validated R² values in my experiment are low (e.g. 0-5%). Should I be concerned?"
  
  The size of the cross-validated R² values in any given dataset depends on a variety of factors, including the amount of noise (thermal, physiological, etc.) in the data, the strength of the evoked BOLD response (which depends on both the underlying neural activity magnitude as well as hemodynamic coupling characteristics in each voxel), and the experimental design (e.g. long-duration conditions will tend to elicit larger BOLD changes than short-duration conditions). In most circumstances, the absolute magnitude of the R² values is probably not of intrinsic interest; rather, it is the estimates of the evoked responses (and their reliability) that is of interest. So, having low R² values is in itself not necessarily a cause for concern (although it can be informative for judging general SNR levels).
  
  To clarify the way cross-validated R² values work, suppose you have a perfect model (i.e. you have infinite data to estimate the parameters of a GLM whose assumptions are valid). Even though this model is perfect, the model may still have low cross-validated R² values. This is because even a perfect model cannot predict noise in unseen data. One way to increase R² values is to reduce noise in the data being predicted, and a simple way to do this is to acquire two (or more) runs with identical experimental conditions (including identical timing) and then average these runs together before proceeding to the GLM analysis. For example, you could collect 5 runs, repeat these 5 runs exactly, average corresponding pairs of runs together, and then submit the averaged 5 runs to GLMdenoise.
  
  
• "How important is the removal of good voxels (voxels with cross-validated R² greater than 0%) from the noise pool? Can we just skip this step?"
  
  You can, in fact, experiment with this aspect of GLMdenoise by setting the opt.brainR2 parameter to, say, 101, which will allow all voxels to enter the noise pool. The reason that it is important to exclude voxels with signals related to the experiment is that otherwise, the noise regressors that are derived will potentially contain signals related to the experiment, and this is likely to diminish the performance gains obtained by introducing noise regressors into the GLM model. Indeed, a comparison of results obtained with and without exclusion of good voxels is provided in the GLMdenoise paper.
  
  
• "Can I use GLMdenoise to denoise resting-state fMRI data?"
  
  Central to GLMdenoise is the idea that we have a signal of interest (i.e. task-related responses) and this signal can be estimated and cross-validated. This is not the case (at least in any straightforward sense) in resting-state fMRI, so GLMdenoise cannot be used for resting-state fMRI.
  

Other notes

Error-checking user inputs. There are currently no safeguards on what happens if the user provides inputs in the wrong format.

Singular matrices. In some cases (e.g., a finite impulse response model with many free parameters and low amounts of data), the design matrix may be singular. The code intentionally crashes if a singular design matrix is encountered.

Reoptimize the noise pool. It is possible that voxels in the noise pool (that have cross-validated R² less than 0%) will, after denoising, have cross-validation R² greater than 0%. In theory, one might suppose that a new noise pool can be constructed (based on the new identification of what voxels are signal and what voxels are noise), new noise regressors can be derived, new models can be fit, etc., and the whole process can be iterated until convergence. This is an interesting idea, but it is doubtful that this would result in any substantial changes/improvements. The reason is that the proportion of voxels that escape the noise pool is probably very low in any given experiment and their time-series data are dominated by noise anyway; thus, removing those voxels from the noise pool will probably not substantially change the noise regressors that are derived.

Error estimation. To obtain error bars on beta weights, GLMdenoise uses a bootstrapping procedure (i.e. draw runs with replacement from the available set of runs, estimate parameters, and repeat this process a large number of times). Since this process is stochastic, error estimates on beta weights may vary a bit, and in particular, may vary across conditions. If, in subsequent analyses, you wish to convert each voxel's beta weights into t-units, instead of dividing each beta weight by its standard error, you may wish to first calculate the average standard error across conditions (for each voxel) and divide all beta weights (associated with that voxel) by this value. This, of course, presumes that the noise is roughly constant across conditions, but it does have the benefit that random fluctuations in error estimates across conditions will not affect the final values obtained for a voxel. GLMdenoise also provides an option for obtaining parametric GLM fits and associated error estimates.

Multiple sessions. If you are attempting to analyze functional data from different scan sessions, it may be useful to apply GLMdenoise to each session individually and then pool the results across sessions. The reason is that signal and noise characteristics may vary substantially from session to session.

Known issues and caveats

Memory usage. The code consists of large-scale matrix operations applied to many voxels simultaneously. This means that the code is fast but memory-intensive. Currently, there are no internal checks on the amount of memory used by the code. Thus, there is potential for the code to hit the maximum memory available on your machine, thereby causing swapping (and unreasonably slow performance). Memory usage is particularly dependent on the number of bootstraps performed (so you may wish to keep the number of bootstraps low, or set the number of bootstraps to zero). To reduce memory usage, you may also want to set opt.denoisespec to {}, make sure your data is prepare in single format, and/or crop your fMRI volumes. The easiest solution may be to buy more RAM!

Unbalanced designs. A presumption of GLMdenoise is that in any given dataset, there are multiple runs and conditions repeat across runs. In addition, there is some presumption that runs are more or less "similar". To understand what this last condition means, let us consider an extreme case. Suppose that some of the runs in a dataset are extremely short (e.g. 30 time points) whereas the remainder of the runs are long (e.g. 300 time points). In this case, we expect some degree of inconsistency with regards to the appropriate amount of denoising to perform across the two types of runs. That is, when training the model on the long runs, the number of PCs that result in optimal performance will probably be on high side, whereas when training the model on the short runs, the number of PCs that result in optimal performance will probably be on the low side (i.e. overfitting is likely).

Unbalanced designs and bootstrapping. Unbalanced designs can interact in certain ways with the bootstrapping procedure. For example, suppose that you have two run types such that a given set of conditions occur in one run type and a non-overlapping set of conditions occur in the other run type. In this case, the bootstrap procedure used at the end of the GLMdenoise algorithm may encounter a bootstrap sample that (by chance) does not include any occurrence of a given condition (for example, suppose that all draws in a bootstrap sample were obtained from runs of the first run type). If the code encounters a case where there are no occurrences of a given condition, the code will simply assign a zero weight for those cases. A solution for the issue of unbalanced designs and bootstrapping is to make appropriate use of the opt.bootgroups variable (that is, you can ensure that the bootstrap sample is balanced with respect to the two types of runs).

Unbalanced designs and cross-validation. The issue of unbalanced designs can also crop up in the leave-one-run-out cross-validation procedure used in GLMdenoise. For example, suppose all occurrences of a certain set of conditions occur in just one of the runs in a dataset. Then, when that run is left out in the cross-validation procedure, then no occurrences of those conditions are available to estimate the beta weights corresponding to those conditions. When this is encountered, the code will simply assign a zero weight for those conditions, thereby resolving the problem (although the situation is a bit strange since the prediction for the left-out run is always a time-series consisting of 0s and so denoising will never appear to be useful for that cross-validation iteration).

Bootstrap smaller chunks of data. The strategy for estimating error bars on model parameters is to bootstrap runs (i.e., draw with replacement from the original set of runs). With small numbers of runs, this strategy might result in sub-optimal estimates. One potential strategy is to split runs into small chunks (e.g. 1-min chunks) and then bootstrap these chunks. This strategy may produce better bootstrap results, and still largely respects the fact that the noise is not independent from time point to time point.